De laatste tijd heb ik mij vaak blauw geërgerd aan Rik Torfs. De man is op twitterkruistocht om de logica in discrediet te brengen. Neem bijvoorbeeld deze tweet:

Of deze:

Bij zulke uitspraken denk ik terug aan mijn humanioriatijd in het Sint-Jan Berchmanscollege te Brussel (een jezuïetencollege, inderdaad). Onze klastitularis in wat toen de poësis heette, laat ik hem Kaesemans noemen, was een groot liefhebber van taal en poëzie. Met wiskunde en wetenschap had hij dan weer een soort haat-liefdeverhouding, zoals die op jezuïetencolleges wel vaker voorkomt.

Op een dag vertelde Kaesemans ons een logische paradox van de griekse wijsgeer Zeno. "Om aan die muur te geraken, moet ik eerst de helft van de afstand afleggen. Daarna de helft daarvan. Daarna weer de helft, en zo voort tot in het oneindige. En dus geraak ik er nooit. Er is geen speld tussen te krijgen. En toch geraak ik er!" Daarop keek Kaesemans de klas rond, genietend van de onuitgesproken triomf. Het besluit lag voor de hand. Met logica alleen geraken we er niet. Om de werkelijkheid te vatten is meer nodig, poëzie bijvoorbeeld.

Ik besefte zeer goed dat Kaesemans en Zeno onzin verkochten. We geraken aan de muur, en dus is er ergens een logische denkfout. Maar waar? Ik kon er toen inderdaad geen speld tussen krijgen. Maar dat was een kwestie van ongelukkige timing. Want de techniek die uiteindelijk tot inzicht zou leiden werd enkele weken later geïntroduceerd in de les wiskunde. Om dat uit te leggen nodig ik u uit om mee te redeneren over onze wandeling naar de muur.

Dit is een voorstelling van de laatste 2 meter:

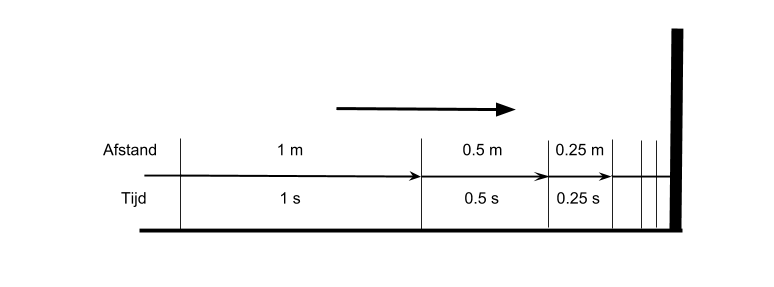
Eerst leggen we 1m af in 1s, dan 0.5m in 0.5s, daarna 0.25ms in 0.25s, enzovoort. De snelheid is de afgelegde afstand gedeeld door de tijd, en die blijft constant:

`(1m)/(1s) = (0.5m)/(0.5s) = (0.25m)/(0.25s) = (0.125m)/(0.125s) ... = 1\ m//s`

Voor elk interval is de snelheid dus 1 m/s. In de wiskunde wordt een interval aangeduid met het symbool Δ. Als we een afstandsinterval noteren met Δx en het overeenkomstig tijdsinterval met Δt kunnen we samenvatten als volgt:

`(\Delta x) / (\Delta t) = 1\ m//s`

Dit geldt voor eender welk interval, hoe klein we het ook maken, ook als het "oneindig klein" wordt. Nu komt de geniale stap. Op een bepaald moment kwamen wiskundigen met het idee om een "oneindig klein" interval expliciet voor te stellen. In de moderne notatie wordt daarvoor de Δ vervangen door een kleine d. Voor onze wandeling naar de muur evolueren afstand en tijd in gelijke mate naar een oneindig klein interval. Dus:

`dx / dt = 1\ m//s`

Deze formule legt de denkfout in Zeno's paradox bloot. De denkfout is dat je wel het interval Δx oneindig klein laat worden, maar niet het tijdsinterval Δt. In dat geval wordt de snelheid 0 en geraak je nooit aan de muur. Maar het klopt natuurlijk niet. Het tijdsinterval Δt wordt even goed oneindig klein en de snelheid blijft wat ze is. Om een oneindig kleine afstand af te leggen, heb je ook slechts een oneindig kleine tijd nodig. Het is de logica zelve eigenlijk, maar je hebt een wiskundig formalisme nodig om het helder te zien.

Oneindig klein is niet hetzelfde als nul - het zou een tweet van een wiskundig onderlegde versie van Rik Torfs kunnen zijn. Wat is het verschil? Het begrip "oneindig klein" bevat informatie over de relaties tussen verschillende oneindig kleine zaken. Stel bijvoorbeeld dat je je snelheid verdubbelt. In het tijdsinterval Δt leg je nu een twee maal grotere afstand Δ2x af. Dus:

`(\Delta 2x) / (\Delta t) = 2\ m//s`

en ook:

`(d2x) / dt = 2\ m//s`

d2x is even goed oneindig klein als dx, maar toch is het twee maal groter. Als je dat niet gelooft, ren dan maar eens met een snelheid van 2 m/s naar die muur toe.

De wiskunde van het oneindige kleine werd ontwikkeld in de 17e eeuw door Isaac Newton and Gottfried Leibniz, twee van de grootste wetenschappers ooit. Voor hun wetenschappelijk werk hadden zij een techniek nodig om het concept verandering wiskundig te beschrijven. Het resultaat staat bekend als infinitesimaalrekenen of calculus en is één van de belangrijkste wiskundige uitvindingen ooit. Moderne wetenschap, zowel theoretische als toegepaste, is ondenkbaar zonder calculus.

Natuurlijk hebben Newton en Leibniz de calculus niet ontwikkeld om Zeno's paradox op te lossen. Maar er is wel een filosofisch verband. Zeno wou aantonen dat verandering een illusie is. Hij gaf het dus al op nog voor het interessant begon te worden. Gelukkig hadden Newton en Leibniz een andere houding. Zij bleven logisch nadenken over het probleem en verder werken aan de doorbraak. Die leidde dan weer tot nieuwe inzichten. Over Zeno's paradox bijvoorbeeld hebben filosofen zich eeuwen het hoofd gebroken, en een paar misschien nog altijd. Maar dankzij de de calculus weten we waarom het helemaal geen paradox is, maar een eenvoudig probleem met een heldere oplossing.

Voor de ware wetenschapper is logica de leidraad, ook voor het onderzoek naar de aard en de limieten van logica en wetenschap zelf. En dat zou de houding van elke intellectueel moeten zijn. Want uiteindelijk vergroot logisch nadenken het inzicht in de werkelijkheid. Vaak komt de doorbraak via de ontwikkeling van een theoretisch model of een wiskundige formulering of techniek. Dat leidt dan weer tot nieuwe practische en theoretische inzichten, in een zelfvoedende positieve spiraal.

Er is wel een groot probleem: logisch nadenken is moeilijk en vraagt veel inspanning. Het "gezond verstand" met zijn handige binnenwegen is dikwijls een slechte raadgever. Zonder goede leermeesters en opleiding is het voor de meesten onder ons een onhaalbare kaart. Als er één instelling is die deze rol kan en moet vervullen, dan is het wel de universiteit. En dat is ook de boodschap die ze zou moeten uitdragen. Maar dat vereist een andere boodschapper dan Rik Torfs, die niet verder komt dan het eloquent getuigen van zijn onbegrip.